Gaetano Fichera

Gaetano Fichera
Gaetano Fichera in 1976 (photo by Konrad Jacobs)
Born	8 February 1922 Acireale
Died	1 June 1996(1996-06-01) (aged 74) Rome
Nationality	Italian
Fields	Mathematics
Institutions	Istituto Nazionale di Alta Matematica, Istituto Nazionale per le Applicazioni del Calcolo, Università di Trieste, Università di Roma
Alma mater	Università di Roma, 1941
Doctoral advisor	Mauro Picone
Doctoral students	see the teaching activity section
Known for	Linear elasticity, variational inequalities, numerical analysis, several complex variables
Influenced	Mathematical analysis, calculus of variation, partial differential equations, numerical analysis, several complex variables
Notable awards	1949 Columbus Prize, 1961 Italian Minister of Education Prize, 1976 Antonio Feltrinelli Prize, 1979 golden medal "Benemeriti della Scuola, della Cultura, dell'Arte" (issued by the President of the Italian Republic), 1982 Ivane Javakhishvili Medal (Tbilisi State University), 1993 medal of the University of Perugia for Foreigners

Gaetano Fichera (8 February 1922 – 1 June 1996) was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables. He was born in Acireale, and died in Rome.

1 Biography
2 Work
- 2.1 Research activity
- 2.2 Teaching activity
3 See also
4 Notes
5 Bibliography
6 References
7 External links

Biography

He was born in Acireale, a town near Catania in Sicily: he was the elder of the four sons of Giuseppe Fichera and Marianna Abate.^[1] His father Giuseppe was a professor of mathematics and influenced the young Gaetano starting his life-long passion. In his young years he was a talented football player. On 1 February 1943 he was in the Italian Army and during the events of September 1943 he was taken prisoner by the Nazist troops, kept imprisoned in Teramo and then sent to Verona: he succeeded in escaping from there and reached the Italian region of Emilia-Romagna, spending with partisans the last year of war. After the war he was first in Rome and then in Trieste, where he met Matelda Colautti, which become his wife in 1952.

Education and academic career

After graduating from the liceo classico in only two years, he entered the University of Catania at the age of 16, being there from 1937 to 1939 and studying under Pia Nalli. Then he went to the university of Rome, where in 1941 he earned his laurea with magna cum laude under the direction of Mauro Picone, when he was only 19. He was immediately appointed by Picone as an assistant professor to his chair and as a researcher at the Istituto Nazionale per le Applicazioni del Calcolo, becoming his pupil. After the war he went back to Rome working with Mauro Picone: in 1948 he became "Libero Docente" (free professor) of mathematical analysis and in 1949 he was appointed as full professor at the University of Trieste. As he remembers in (Fichera 1991, p. 14), in both cases one of the members of the judging commission was Renato Caccioppoli, which become a close friend of him. From 1956 onward he was full professor at the University of Rome in the chair of mathematical analysis and then at the Istituto Nazionale di Alta Matematica in the chair of higher analysis, succeeding to Luigi Fantappiè. He retired from university teaching in 1992,^[2] but was professionally very active until his death in 1996: particularly, as a member of the Accademia Nazionale dei Lincei and first director of the journal Rendiconti Lincei – Matematica e Applicazioni^[3] he succeeded in reviving the reputation of this publication.^[4]

Honours

He was a member of several academies, notably of the Accademia Nazionale dei Lincei, the Accademia Nazionale delle Scienze detta dei XL and of the Russian Academy of Science.

Teachers

His lifelong friendship with his teacher Mauro Picone is remembered by him in several occasions. As recalled by Colautti Fichera (2006, pp. 13–14), his father Giuseppe was an assistant professor to the chair of Picone while he was teaching at the University of Catania: they become friends and their friendship lasted even when Giuseppe was forced to leave the academic career for economic reasons, being already the father of two sons, until Giuseppe's death. The young, in effect child, Gaetano, was kept by Picone in his arms. From 1939 to 1941 the young Fichera developed his research directly under the supervision of Picone: as he remembers, it was a time of intense work. But also, when he was back from the front in April 1945^[5] he met Picone while he was in Roma in his way back to Sicily, and his advisor was so happy to see him as a father can be seeing its living child. Another mathematician Fichera was influenced by and acknowledged as one of his teachers and inspirators was Pia Nalli: she was an outstanding analyst, teaching for several years at the University of Catania, being his teacher of mathematical analysis from 1937 to 1939. Antonio Signorini and Francesco Severi were two of Fichera's teachers of the Roman period: the first one introduced him and inspired his research in the field of linear elasticity while the second inspired his research in the field he taught him i.e. the theory of analytic functions of several complex variables. Signorini had a strong long-time friendship with Picone: on a wall of the apartment building where they lived, in Via delle Tre Madonne, 18 in Rome, a memorial tablet which commemorates the two friends is placed, as Fichera (1995b, p. 47) recalls. The two great mathematicians extended their friendship to the young Fichera, and as a consequence this led to the solution of the Signorini problem and the foundation of the theory of variational inequalities. Fichera's relations with Severi were not as friendly as with Signorini and Picone: nevertheless, Severi, which was one of the most influential Italian mathematicians of the first half of the 20th century, esteemed the young mathematician. During a course on the theory of analytic functions of several complex variables taught at the Istituto Nazionale di Alta Matematica from the fall of 1956 and the beginning of the 1957, whose lectures were collected in the book (Severi 1958), Severi posed the problem of generalizing his theorem on the Dirichlet problem for holomorphic function of several variables, as Fichera (1957, p. 707) recalls: the result was the paper (Fichera 1957), which is a masterpiece, although not generally acknowledged for various reasons described by Range (2002, pp. 6–11). Other scientists he had as teachers during the period 1939–1941 were Enrico Bompiani, Leonida Tonelli and Giuseppe Armellini: he remembered them with great respect and admiration, even if he did not share all their opinions and ideas, as Colautti Fichera (2006, p. 16) recalls.

Friends

A complete list of Fichera's friends includes some of the best scientists and mathematicians of the 20th century: Olga Oleinik, Olga Ladyzhenskaya, Israel Gel'fand, Ivan Petrovsky, Vladimir Maz'ya, Nikoloz Muskhelishvili, Ilia Vekua, Richard Courant, Fritz John, Kurt Friedrichs, Peter Lax, Louis Nirenberg, Ronald Rivlin, Hans Lewy, Clifford Truesdell, Edmund Hlawka, Ian Sneddon, Jean Leray, Alexander Weinstein, Alexander Ostrowski, Renato Caccioppoli, Solomon Mikhlin, Paul Naghdi, Marston Morse were among his friends, scientific collaborators and correspondents, just to name a few. He build up such a network of contacts being invited several times to lecture on his research by various universities and research institutions, and also participating to several academic conferences, always upon invitation. This long series of scientific journeys started in 1951, when he went to the USA together with his master and friend Mauro Picone and Bruno de Finetti in order to examine the capabilities and characteristics of the first electronic computers and purchase one for the Istituto Nazionale per le Applicazioni del Calcolo: the machine they advised to purchase was the first computer ever working in Italy. The most complete source about his friends and collaborators is the book (Colautti Fichera 2006) by his wife Matelda: in those reference it is also possible to find a fairly complete description of Gaetano Fichera's scientific journeys.

The close fiendship between Angelo Pescarini and Fichera has not his roots in their scientific interests: it is another war story. As Oleinik (1997, p. 12) recalls, Gaetano, being escaped from Verona and hidden in a convent in Alfonsine, tried to get in touch with the local group of partisans in order to help the people of that town who had been so helpful with him: they were informed about an assistant professor to the chair of higher analysis in Rome who was trying to reach them. Angelo, which was a student of mathematics at the University of Bologna under Gianfranco Cimmino, a former pupil of Mauro Picone, was charged of the task of testing the truth of Gaetano's assertions, examining him in mathematics: his question was:– "Mi sai dire una condizione sufficiente per scambiare un limite con un integrale (Can you give me a sufficient condition for interchanging limit and integration)?"–. Gaetano quickly answered:– "Non solo ti darò la condizione sufficiente, ma ti darò anche la condizione necessaria e pure per insiemi non limitati (I can give you not only a sufficiet condition, but also a necessary condition, and not only for bounded domains, but also for unbounded domains)"–. In effect, Fichera proved such a theorem in the paper (Fichera 1943), his latest paper written in while he was in Rome before joining the army: from that moment on he often used to joke saying that good mathematicians can always have a good application, even for saving one's life.

One of his best friends and appreciated scientific collaborator was Olga Arsenievna Oleinik: she cured the redaction of his last posthumous paper (Fichera 1997), as Colautti Fichera (2006, pp. 202–204) recalls. Also, she used to discuss his work with Gaetano, as he did with her: sometimes their discussion become lively, but nothing more, since they were extremely good friends and estimators of each one's work.

Work

Research activity

He is the author of more than 250 papers and 18 books (monographs and course notes): his work concerns mainly the fields of pure and applied mathematics listed below. A common characteristic to all of his research is the use of the methods of functional analysis to prove existence, uniqueness and approximation theorems for the various problems he studied, and also a high consideration of the analytic problems related to problems in applied mathematics.

Mathematical theory of elasticity and variational inequalities. In the elasticity theory, Fichera is known for the paper (Fichera 1961c) where he proves the "Fichera maximum principle", and for his work on variational inequalities, started with the paper (Fichera 1963), where he announced the existence and uniqueness theorem for the Signorini problem, and ended with the subsequent ones (Fichera 1964a) and (Fichera 1964b), where the full proof was published: those papers are the founding works of the field of variational inequalities, as remarked by Stuart Antman in (Antman 1983, pp. 282–284).^[6] Concerning the Saint-Venant's principle, he was able to prove it using a variational approach and a slight variation of a technique employed by Richard Toupin to study the same problem: in the paper (Fichera 1979a)^[7] there is a complete proof of the principle under the hypothesis that the base of the cylinder is a set with piecewise smooth boundary. Also he is known for his researches in the theory of hereditary elasticity: the paper (Fichera 1979b) emphasizes the necessity of analyzing very well the constitutive equations of materials with memory in order to introduce models where an existence and uniqueness theorems can be proved in a such a way that the proof does not rely on an implicit choice of the topology of the function space where the problem is studied. At last, it is worth to mention that Clifford Truesdell invited him to write the contributions (Fichera 1972a) and (Fichera 1972b) for Siegfried Flügge's Handbuch der Physik.
Partial differential equations: he developed an abstract approach through functional analysis to study general boundary value problems for linear partial differential equations, proving in the paper (Fichera 1955a) a theorem similar in spirit to the Lax–Milgram theorem. He studied deeply the mixed boundary value problem i.e. a boundary value problem where the boundary has to satisfy a mixed boundary condition: in his first paper on the topic, (Fichera 1949), he proves the first existence theorem for the mixed boundary problem for self-adjoint operators of 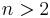$n>2$ variables, while in the paper (Fichera 1955a, pp. 22–29) he proves the same theorem dropping the hypothesis of self-adjointness. He is, according to Oleinik (1997), the founder of the theory of partial differential equations of non-positive characteristics: in the paper (Fichera 1956) he introduced the now called Fichera's function, in order to identify subsets of the boundary of the domain where the boundary value problem for such kind of equations is posed, where it is necessary or not to specify the boundary condition: another account of the theory can be found in the paper (Fichera 1960), which is written in English and was later translated in Russian and Hungarian.^[8]
Calculus of variation: his contributions to the calculus of variation are mainly devoted to the proof of existence and uniqueness theorems for maxima and minima of functionals of particular form, in conjunction with his studies on variational inequalities and linear elasticity in theoretical and applied problems: in the paper (Fichera 1964a) a semicontinuity theorem for a functional introduced in the same paper is proved in order to solve the Signorini problem, and this theorem was extended in (Fichera 1964c) to the case where the given functional has general linear operators as arguments, not necessarily partial differential operators.
Functional analysis and eigenvalue theory. It is difficult to single out his contributions to functional analysis since, as stated at the beginning of this section, the methods of functional analysis are ubiquitous in his research: however, it is worth to remember paper (Fichera 1955a), where an important existence theorem is proved. His contributions in the field of eigenvalue theory began with the paper (Fichera 1955b), where he formalizes a method developed by Mauro Picone for the approximation of eigenvalues of operators subject only to the condition that their inverse is compact: however, as he admits in (Fichera 1974a, pp. 13–14), this method does not give any estimate on the approximation error on the value of the calculated (approximated) eigenvalues. He contributed also to the classical eigenvalue problem for symmetric operators, introducing the method of orthogonal invariants: details on this method can be find in (Fichera 1974a, pp. 33–127), (Fichera 1978a), (Weinberger 1999) and references therein.
Approximation theory. His work in this field is mainly related to the study of systems of functions, possibly being particular solutions of a given partial differential equation or system of such equations, in order to prove their completeness on the boundary of a given domain. The interest of this research is obvious: given such a system of functions, every solution of a boundary value problem can be approximated by an infinite series or Fourier type integral in the topology of a given function space. One of the most famous examples of this kind of theorem is Mergelyan's theorem, which completely solves the problem in the class of holomorphic functions for a compact set in the complex plane. In his paper (Fichera 1948), Fichera studies this problem for harmonic functions,^[9] relaxing the smoothness requirements on the boundary in the already cited work (Fichera 1955a): a survey on his and others' work in this area, including contributions of Mauro Picone, Bernard Malgrange, Felix Browder and a number of other mathematicians, is contained in the paper (Fichera 1979c). Another branch of his studies on approximation theory is strictly tied to complex analysis in one variable, and to the already cited Mergelyan's theorem: he studied the problem of approximating continuous functions on a compact set (and analytic on its interior if this is non void) of the complex plane by rational functions with prescribed poles, simple or not. The paper (Fichera 1974b) surveys the contribution to the solution of this and related problems by Sergey Mergelyan, Lennart Carleson, Gábor Szegö as well as others, including his own.
Potential theory: his contributions in this field are very important. The results of his paper (Fichera 1948) occupy paragraph 24 of chapter II of the textbook (Günther 1967, pp. 108–117), as remarked by in Oleinik (1997, p. 11). Also, his researches (Fichera 1975) and (Fichera 1976) on the asymptotic behaviour of the electric field near singular points of the conducting surface, widely known among the specialists (as several works of V.G. Maz'ya, S.A. Nazarov, B.A. Plamenevsky, B.W. Schulze and others testify) can be included in between his works in potential theory.
Measure theory and integration: his main contributions are contained in the papers (Fichera 1943) and (Fichera 1954). In the first one he proves that a condition on a sequence of integrable functions previously introduced by Mauro Picone is both necessary and sufficient in order to assure that limit process and the integration process commute, both in bounded and unbounded domains: the theorem is similar in spirit to the dominated convergence theorem, which however only states a sufficient condition. The second paper contains an extension of the Lebesgue's decomposition theorem to finitely additive measures: this extension required him to generalize of the Radon–Nykodim derivative, requiring it to be a set function belonging to a given class and minimizing a particular functional.
Complex analysis: he contributed to both the classical topic of complex analysis in one variable and the more recent one of complex analysis in several variables. His contributions to complex analysis in one variable are essentially approximation results, well described in the survey paper (Fichera 1974b) (see also the section about his contributions in approximation theory). In the field of functions of several complex variables variables, his contributions were outstanding,^{[says who?]} but also not generally acknowledged (see the paper (Range 2002) for the details). Precisely, he solved the Dirichlet problem for holomorphic function of several variables under the hypothesis that the boundary of the domain 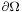$\scriptstyle\partial\Omega$ has a Holder continuous normal vector (i.e. it is of 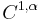$C^{1,\alpha}$ class) and the Dirichlet boundary condition is a function belonging to the Sobolev space 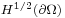$\scriptstyle H^{1/2}(\partial\Omega)$ satisfying the weak form of the tangential Cauchy–Riemann condition (introduced by him) in the paper (Fichera 1957) (see also (Fichera1986), where the theorem is presented in English and extended to the case that the normal vector and the Dirichlet boundary condition are only continuous), extending a previous result of Francesco Severi: this theorem and the Lewy–Kneser theorem on the local Cauchy problem for holomorphic functions of several variables, laid the foundations of the theory of CR-functions. Another important result is his proof in (Fichera 1983) of an extension of Morera theorem to functions of several complex variables, under the hypothesis that the given function $f$ is only locally integrable: previous proofs under more restrictive assumptions were given by Francesco Severi in (Severi 1931) and Salomon Bochner in (Bochner 1953). He also studied the properties of the real part and imaginary part of functions of several complex variables, i.e. 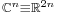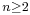pluriharmonic functions: starting from the paper (Amoroso 1912) he gives a trace condition analogous to the tangential Cauchy–Riemann condition for the solvability of the Dirichlet problem for pluriharmonic functions in the paper (Fichera 1982a), and generalizes a theorem of Luigi Amoroso to the complex vector space $\scriptstyle \mathbb{C}^n\equiv\mathbb{R}^{2n}$ for $\scriptstyle n\geq 2$ complex variables in the paper (Fichera 1982b). Also he was able to prove that a integro-differential equation defined on the boundary of a smooth domain by Luigi Amoroso in his cited paper, the Amoroso integro-differential equation, is a necessary and sufficient condition for the solvability of the Dirichlet problem for pluriharmonic functions when this domain is the sphere in $\scriptstyle \mathbb{C}^2\equiv\mathbb{R}^4$ : details can be found in the paper (Fichera 1982c).
Exterior differential forms. His contributions to the theory of differential forms starts as a war story^[10]: having read a famous memory of Enrico Betti (where Betti numbers were introduced) just before joining the army, he used this knowledge in order to develop a theory of exterior differential forms while he was kept prisoner in Teramo jail. This fact is not uncommon in talented people being kept in captivity, as the known experience of Jean Leray with sheaf theory shows. When he was back in Rome in 1945, he discussed his discovery with Enzo Martinelli, who very tactfully informed him that the idea was already developed by mathematicians Élie Cartan and Georges de Rham. However, he continued work on this theory, contributing with several papers, and also advised all of his students to study it, despite from the fact of being an analyst, as he remarks: his main results are collected in the papers (Fichera 1961a) and (Fichera 1961b). In the first one he introduced k-measures, a concept less general than currents but easier to work with: his aim was to clarify the analytic structure of currents and to prove all relevant results of the theory i.e. the three theorems of de Rham and Hodge theorem on harmonic forms in a simpler, more analytic way. In the second one he developed an abstract Hodge theory, following the axiomatic method, proving an abstract form of Hodge theorem.
Numerical analysis. As already said in a previous section, his main direct contribution to the field of numerical analysis is the introduction of the method of orthogonal invariants for the calculus of eigenvalues of symmetric operators: however, as already remarked in the introduction to this section, it is hard to find something in his works which is not related to applications. As an example, his works on partial differential equations and linear elasticity have always a constructive aim: for example, the results of paper (Fichera 1975) which deals with the asymptotic analysis of the potential were included in the book (Fichera 1978a) and led to the definition of the Fichera corner problem as a standard benchmark problem for numerical methods. For this aspect, see also the recollections of Wendland in (Wendland 2007, p. 8). Another example of his work on quantitative problems is the interdisciplinary work surveyed in (Fichera 1978b).^[11]
Biographies and historical studies: his work in this field occupy all the volume (Fichera 2002). He wrote bibliographical sketches for a number of mathematicians, both teachers, friends and collaborators, including Mauro Picone, Luigi Fantappiè, Pia Nalli, Maria Adelaide Sneider, Renato Caccioppoli, Solomon Mikhlin, Francesco Tricomi, Alexander Weinstein, Aldo Ghizzetti. His historical works contain several observations against the so called historical revisitation: the meaning of this concept is clearly stated in the paper (Fichera 1996). He identifies with the word revisitation the analysis of historical facts basing only on modern conceptions and points of view: this kind of analysis differs from the "true" historical one since it is heavily affected by the historian's point of view. The historian applying this kind of methodology to history of mathematics, and more generally to the history of science, emphasizes the sources that have led a field to its modern shape, neglecting the efforts of the pioneers.

Teaching activity

His teaching activity was almost as intense as his research actvity: he also was a pioneer in encouraging gifted women to choose a career in mathematical research, as Weinberger (1999, p. 51) recalls. An almost complete list of his doctoral students is reported below:

Lucilla Bassotti
Caterina Cassisa
Pieranita Castellani Rizzonelli
Alberto Cialdea
Maria Pia Colautti
Luciano De Vito
Flavia Lanzara
Umberto Mosco
Paolo Emilio Ricci
Mirella Schaerf
Maria Adelaide Sneider
Giuseppe Tomassini

Notes

^ The main reference about his personal life is the book (Colautti Fichera 2007).
^ His last lesson of the course of higher analysis was published in (Fichera 1995a).
^ This scientific journal is the follow-up of the older and glorious Atti dell'Accademia Nazionale dei Lincei – Classe di Scienze Fisiche, Matematiche, Naturali, the official publication of the Accademia Nazionale dei Lincei.
^ See Colautti Fichera (1997, p. 14, footnote), and Galletto (2007, p. 142).
^ The episode is narrated in (Colautti Fichera 2006, pp. 30–31).
^ These are his only papers in the field of variational inequalities: see the article "Signorini problem" for a discussion of the reasons why he left this field of research.
^ The same paper was previously published in Russian in a volume in honour of Ilia Vekua: see Colautti Fichera (1997, p. 29) for the exact reference.
^ See the bibliography (Colautti Fichera 1997): some of the translated papers are available online from the All-Russian Mathematical Portal.
^ See also the monograph (Günther 1967).
^ He tells this story in his last lesson (Fichera 1995a, pp. 18–19): see also (Colautti Fichera 2006, p. 21).
^ See also the paper (Fichera, Sneider & Wyman 1977), where methods of mathematical analysis and numerical analysis are applied to a problem posed by biological sciences.

Bibliography

Antman, Stuart (1983), "The influence of elasticity in analysis: modern developments", Bulletin of the American Mathematical Society 9 (3): 267–291, doi:10.1090/S0273-0979-1983-15185-6, MR 714990, Zbl 0533.73001 . A historical paper about the fruitful interaction of elasticity theory and mathematical analysis: the creation of the theory of variational inequalities by G. Fichera is described in paragraph 5, pages 282–284.
Cialdea, Alberto, ed. (2000) (in English and Italian), Homage to Gaetano Fichera, quaderni di matematica, 7, Rome: Aracne Editrice, pp. xiv+347, MR 1913523, Zbl 0982.00057, http://www.dimat.unina2.it/quaderni/quaderni07.htm . A volume published by the Department of mathematics the Seconda Università degli Studi di Napoli in its journal "Quaderni di matematica", dedicated to the memory of Gaetano Fichera: the contributions, written by his pupils, friends and collaborators, deal about topics that inspired Fichera's scientific work.
Colautti Fichera, Matelda (1997), "Elenco delle pubblicazioni di Gaetano Fichera (List of the publications of Gaetano Fichera)", Atti della Accademia Nazionale dei Lincei, Rendiconti Lincei, Matematica e Applicazioni, 9 8 (1): 14–33 .
Colautti Fichera, Matelda (2007) (in Italian), ... ed è subito sera... La lunga, brevissima vita di Gaetano Fichera (The long, extremely short life of Gaetano Fichera), Roma: Self-published, pp. 217 . The story of the life of Gaetano Fichera written by his wife, Matelda Colautti Fichera. The first, untranslated phrase of the title is the last verse (and title) of a famous poem of Salvatore Quasimodo, and was the concluding phrase of the last lesson of Fichera, in the occasion of his retirement from university teaching in 1992, published in (Fichera 1995a).
Fichera, Gaetano (2002) (in English and Italian), Opere storiche biografiche, divulgative (Historical, biographical, divulgative works), Napoli: Giannini / Società Nazionale di Scienze, Lettere e Arti in Napoli, pp. 491, http://www.socnazsla.unina.it/italiano/fismat/pubbl.htm . A volume collecting works of Gaetano Fichera in the fields of history of mathematics and scientific divulgation.
Fichera, Gaetano (2004) (in Italian), Opere scelte (Selected works), Firenze: Edizioni Cremonese (distributed by Unione Matematica Italiana), pp. XXIX+432 (vol. 1), pp. VI+570 (vol. 2), pp. VI+583 (vol. 3) ISBN 88-7083-811-0 (vol. 1), ISBN 88-7083-812-9 (vol. 2), ISBN 88-7083-813-7 (vol. 3). Three volumes collecting the most important mathematical papers of Gaetano Fichera, with a biographical sketch of Olga A. Oleinik.
Galletto, Dionigi (2007), "Ricordo di Gaetano Fichera a dieci anni dalla morte (Recollection of Gaetano Fichera ten years after the death)" (in Italian), Atti Ufficiali dell'Accademia delle Scienze di Torino 2004–2006: 135–142, http://www.accademiadellescienze.it/media/679 , available from the Accademia delle Scienze di Torino.
Grioli, Giuseppe (1996), "Ricordo di Gaetano Fichera (Remembrance of Gaetano Fichera)" (in Italian), Rendiconti della Accademia Nazionale delle Scienze detta dei XL, Memorie di Matematica e Applicazioni, Serie 5, 20 (1): 221–224, MR 1438747, Zbl 0942.01023, http://www.accademiaxl.it/Biblioteca/Pubblicazioni/browser.php?VoceID=2706 .
Maz'ya, Vladimir (2000), "In memory of Gaetano Fichera", in Ricci, Paolo Emilio, Problemi attuali dell’analisi e della fisica matematica. Atti del II simposio internazionale (Taormina, 15–17 ottobre 1998). Dedicato alla memoria del Prof. Gaetano Fichera., Roma: Aracne Editrice, pp. 1–4, MR 1809014, Zbl 0977.01027 .Some vivid recollection about Gaetano Fichera by his colleague and friend Vladimir Gilelevich Maz'ya.
Oleinik, Olga A. (1997), "The life and scientific work of Gaetano Fichera", Atti della Accademia Nazionale dei Lincei, Rendiconti Lincei, Matematica e Applicazioni, Serie IX, 8 (1): 9–14 . The biographical sketch of Olga A. Oleinik which is included in the first volume of the selected works of Gaetano Fichera, and in the volume of the historical, biographical, and divulgative works. It includes an almost complete list of the works of Fichera, cured by Matelda Fichera Colautti.
Range, R. Michael (2002), "Extension phenomena in multidimensional complex analysis: correction of the historical record", The Mathematical Intelligencer 24 (2): 4–12, doi:10.1007/BF03024609, MR 1907191 . An historical paper correcting some inexact historical statements in the theory of holomorphic functions of several variables, particularly concerning contributions of Gaetano Fichera and Francesco Severi.
Range, R. Michael (2010), "Some landmarks in the history of the tangential Cauchy Riemann equations", Rendiconti di Matematica e delle Sue Applicazioni 30 (3–4): 275–283, MR 2830305, Zbl pre05954009, http://www.mat.uniroma1.it/ricerca/rendiconti/2010%283-4%29/275-283.pdf . An historical paper exploring further the same topic previously dealt in the paper (Range 2002) by the same author.
Wendland, Wolfgang L. (2007), "In memory of Gaetano Fichera", Le Matematiche LXII (II): 7–9, MR 2401174, http://www.dmi.unict.it/ojs/index.php/lematematiche/article/view/24 . Some recollections of the author about Gaetano Fichera.

References

All the works of Gaetano Fichera listed in this section, except (Fichera 1964a), (Fichera 1974a) and also its translation (Fichera 1978a), can be found in his "opere scelte" (Fichera 2004) or in the volume (Fichera 2002).

Amoroso, Luigi (1912), "Sopra un problema al contorno (About a boundary value problem)", Rendiconti del Circolo Matematico di Palermo 33 (1): 75–85, doi:10.1007/BF03015289, JFM 43.0453.03 (in Italian). The first paper where a set of (fairly complicate) necessary and sufficient conditions for the solvability of the Dirichlet problem for holomorphic functions of several variables is given: the bounded domain where the problem is posed and solved is assumed to be not pseudoconvex.
Bochner, Salomon (1953), "The theorem of Morera in several variables", Annali di Matematica Pura e Applicata 34 (1): 27–39, doi:10.1007/BF02415323, Zbl 0052.30703 .
Fichera, Gaetano (1943), "Intorno al passaggio al limite sotto il segno d'integrale (About the passage to the limit under the sign of integral)", Portugaliae Mathematica 4 (1): 1–20, MR 0009192, Zbl 0063.01364, http://purl.pt/2124 (in Italian). A paper containing the theorem on the necessary and sufficient conditions for the exchange of the limit and the integration operations for sequences of functions in the spirit of Henri Lebesgue's Dominated convergence theorem (which, however states only a sufficient condition).
Fichera, Gaetano (1948), "Teoremi di completezza sulla frontiera di un dominio per taluni sistemi di funzioni (Completeness theorems on the boundary of a domain for certain systems of functions)", Annali di Matematica Pura e Applicata, 4 27 (1–2): 1–28, doi:10.1007/BF02415556, Zbl 0035.34801 (in Italian). A now classical paper in potential theory.
Fichera, Gaetano (1949), "Analisi esistenziale per le soluzioni dei problemi al contorno misti, relativi all'equazione e ai sistemi di equazioni del secondo ordine di tipo ellittico, autoaggiunti (Existential analysis of the solutions of mixed boundary value problems, related to second order elliptic equation and systems of equations, selfadjoint)", Annali della Scuola Normale Superiore, III 1 (1–4): 75–100, Zbl 0035.18603, http://www.numdam.org/numdam-bin/fitem?id=ASNSP_1949_3_1_1-4_75_0 (in Italian). The paper containing the first existence and uniqueness theorems for the mixed boundary value problem in fairly general domains.
Fichera, Gaetano (1954), "Sulla derivazione delle funzioni additive d'insieme (On the differentiation of additive set functions)", Rendiconti del Seminario Matematico della Università di Padova 23: 366–397, Zbl 0058.28302, http://www.numdam.org/item?id=RSMUP_1954__23__366_0 (in Italian).
Fichera, Gaetano (1955a), "Alcuni recenti sviluppi della teoria dei problemi al contorno per le equazioni alle derivate parziali lineari (Some recent developments of the theory of boundary value problems for linear partial differential equations)", in Fichera, G., Convegnio Internazionale sulle Equazioni Lineari alle Derivate Parziali – Trieste 25–28 Agosto 1954, Rome: Edizioni Cremonese, pp. 174–227, Zbl 0068.31101 (in Italian). The paper detailing Fichera's approach to a general theory of boundary value problems for linear partial differential equations through a theorem similar in spirit to the Lax–Milgram theorem: as an application, the general existence and uniqueness theorems of paper (Fichera 1949) are proved dropping the hypothesis of self-adjointness, for the linear partial differential operators considered.
Fichera, Gaetano (1955b), "Su un metodo del Picone per il calcolo degli autovalori e delle autosoluzioni (On a method of Picone for the calculus of eigenvalues and eigensolutions)", Annali di Matematica Pura e Applicata, 4 40 (1): 239–259, doi:10.1007/BF02416536, Zbl 0065.35501 (in Italian).
Fichera, Gaetano (1956), "Sulle equazioni differenziali lineari ellittico-paraboliche del secondo ordine (On linear elliptic-parabolic equations of second order)", Memorie della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 5 (1): 1–30, Zbl 0075.28102 (in Italian). The first paper on the theory of partial differential equations of non positive characteristics: the Fichera's function is introduced and its applications to the boundary value problems for this class of operators is detailed. Also the well posedness is considered.
Fichera, Gaetano (1957), "Caratterizzazione della traccia, sulla frontiera di un campo, di una funzione analitica di più variabili complesse (Characterization of the trace, on the boundary of a domain, of an analytic function of several complex variables)", Rendiconti della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 22 (6): 706–715, MR 0093597, Zbl 0106.05202 (in Italian). An epoch-making paper in the theory of CR-functions, where the Dirichlet problem for analytic functions of several complex variables is solved for general data.
Fichera, Gaetano (1961a), "Spazi lineari di k-misure e di forme differenziali (Linear spaces of $k$ -measures and differential forms)", Proceedings of the Symposium on Linear Spaces, Jerusalem, 1960, Jerusalem: Jerusalem Academic Press, pp. 175–226, Zbl 0126.17801 (in Italian). Maybe the most important contribution of Gaetano Fichera to the theory of exterior differential forms: k-measures are introduced and, despite being less general than currents and thus being easier to work with, it is proved that all the most important results of the theory can be obtained using them.
Fichera, Gaetano (1960), "On a unified theory of boundary value problems for elliptic-parabolic equations of second order", in Langer, Rudolph E., Boundary Problems in Differential Equations, Madison: The University of Wisconsin Press, pp. 97–120, Zbl 0122.33504 . A paper about the boundary value problem for partial differential equations of non positive characteristics, where the Fichera's function is introduced and its application are described.
Fichera, Gaetano (1961b), "Teoria assiomatica delle forme armoniche (Axiomatic theory of harmonic forms)", Rendiconti di Matematica e delle sue applicazioni, 5 20: 147–171, MR 0140124, Zbl 0116.07601 (in Italian). A paper containing an abstract theory harmonic forms in Hilbert spaces, including a proof of Hodge theorem.
Fichera, Gaetano (1961c), "Il teorema del massimo modulo per l'equazione dell'elastostatica tridimensionale (The maximum modulus theorem for the three-dimensional elastostatic equation)", Archive for Rational Mechanics and Analysis 7 (5): 373–387, Bibcode 1961ArRMA...7..373F, doi:10.1007/BF00250770, Zbl 0100.30801 (in Italian). The paper where the "Fichera maximum principle" is proved.
Fichera, Gaetano (1963), "Sul problema elastostatico di Signorini con ambigue condizioni al contorno (On the elastostatic problem of Signorini with ambiguous boundary conditions)", Rendiconti della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 34 (2): 138–142, Zbl 0128.18305 (in Italian). A short paper describing briefly the approach to the solution of the Signorini problem.
Fichera, Gaetano (1964a), "Problemi elastostatici con vincoli unilaterali: il problema di Signorini con ambigue condizioni al contorno (Elastostatic problems with unilateral constraints: the Signorini problem with ambiguous boundary conditions)", Memorie della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 7 (2): 91–140, Zbl 0146.21204 (in Italian). The paper containing the existence and uniqueness theorem for the Signorini problem.
Fichera, Gaetano (1964b), "Elastostatic problems with unilateral constraints: the Signorini problem with ambiguous boundary conditions", Seminari dell'istituto Nazionale di Alta Matematica 1962–1963, Rome: Edizioni Cremonese, pp. 613–679 . An English translation of the previous paper.
Fichera, Gaetano (1964c), "Semicontinuity of multiple integrals in ordinary form", Archive for Rational Mechanics and Analysis 17 (5): 339–352, Bibcode 1964ArRMA..17..339F, doi:10.1007/BF00250470, Zbl 0128.10003 . A paper where a semicontinuity theorem is proved for a functional depending on general linear operators (not simply partial differential operators).
Fichera, Gaetano (1972a), "Existence theorems in elasticity", in Flügge, Siegfried; Truesdell, Clifford A., Festkörpermechanik/Mechanics of Solids, Handbuch der Physik (Encyclopedia of Physics), VIa/2, Berlin–Heidelberg–New York: Springer-Verlag, pp. 347–389, Zbl 0277.73001 .
Fichera, Gaetano (1972b), "Boundary value problems of elasticity with unilateral constraints", in Flügge, Siegfried; Truesdell, Clifford A., Festkörpermechanik/Mechanics of Solids, Handbuch der Physik (Encyclopedia of Physics), VIa/2 (paperback 1984 ed.), Berlin–Heidelberg–New York: Springer-Verlag, pp. 391–424, ISBN 3-540-13161-2, ISBN 0-387-13161-2, Zbl 0277.73001 . The encyclopedic voice about problems with unilateral constraints (the class of boundary value problems the Signorini problem belongs to) he wrote for the Handbuch der Physik on invitation by Clifford Truesdell.
Fichera, Gaetano (1974a), "Metodi e risultati concernenti l'analisi numerica e quantitativa (Methods and results concerning numerical and quantitative analysis)", Memorie della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 12 (1): 1–202, Zbl 0334.65002 (in Italian). An extensive survey on some problems of numerical analysis (and associate problems of mathematical analysis) studied by Gaetano Fichera and his group of students: its updated English translation is (Fichera 1978a).
Fichera, Gaetano (1974b), "On the approximation of analytic functions by rational functions", Journal of Mathematical and Physical Science (Madras) 8 (1): 7–19, Zbl 0294.30034 . A survey paper about the theory of approximation of and by analytic functions of a complex variable.
Fichera, Gaetano (1975), "Comportamento asintotico del campo elettrico e della densità elettrica in prossimità dei punti singolari della superficie conduttore (Asymptotic behaviour of the electric field and density of the electric charge in the neighbourhood of singular points of a conducting surface)", Rendiconti del Seminario Matematico dell'Università e Politecnico di Torino 32 (1973–74): 111–143, Zbl 0318.35007 (in Italian). An important paper on the asymptotic analysis of the electric field near the vertex of a conical conducting surface: a freely consultable Russian translation is available here.
Fichera, Gaetano (1976), "Asymptotic behaviour of the electric field near the singular points of the conductor surface", Rendiconti della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 60 (1): 13–20, Zbl 0364.35004 .
Fichera, Gaetano; Sneider, Maria Adelaide; Wyman, Jeffreys (1977), "On the existence of a steady state in a biological system", PNAS 74 (10): 4182–4184, doi:10.1073/pnas.74.10.4182 . A research announcement related to the survey paper (Fichera 1978b).
Fichera, Gaetano (1978a), Numerical and quantitative analysis. Translated from Italian by Sandro Graffi, Surveys and Reference Works in Mathematics, 3, London–San Francisco–Melbourne: Pitman, ISBN 0272002848, Zbl 0384.65043 . An English updated translation of the memoir (Fichera 1974a).
Fichera, Gaetano (1978b), "Un problema di analisi matematica proposto dalla biologia (A problem in mathematical analysis proposed by biology)", Rendiconti di Matematica e delle sue applicazioni, 6 10 (4): 1–6, Zbl 0378.34039 (in Italian). A paper surveying an interdisciplinary research by him, Maria Adelaide Sneider and Jeffries Wyman, on the existence of a steady state in a biological system. (Simoni, RD; Hill, RL; Vaughan, M (2002), "Protein chemistry and the development of allosterism: Jeffries Wyman", The Journal of biological chemistry 277 (46): E34, PMID 12426446.
Fichera, Gaetano (1979a), "Remarks on Saint-Venant's principle", Rendiconti di Matematica e delle sue applicazioni, 6 12: 181–200, Zbl 0443.73002 . A paper containing a mathematical proof of the Saint-Venant's principle.
Fichera, Gaetano (1979b), "Avere una memoria tenace crea gravi problem (Having a tenacious memory creates serious problems)", Archive for Rational Mechanics and Analysis 70 (2): 373–387, Bibcode 1979ArRMA..70..373., doi:10.1007/BF00281161, Zbl 0425.73002 (in Italian).
Fichera, Gaetano (1979c), "The problem of the completeness of systems of particular solutions of partial differential equations", in Ansorge, R.; Glashoff, K.; Werner, B., Numerical mathematics, Symposium on the Occasion of Retirement of Lothar Collatz, Hamburg 1979, International Series of Numerical Mathematics, 49, Basel: Birkhäuser-Verlag, pp. 25–41, Zbl 0434.35010 .
Fichera, Gaetano (1982a), "Problemi al contorno per le funzioni pluriarmoniche (Boundary value problems for pluriharmonic functions)" (in Italian), Atti del Convegno celebrativo dell'80° anniversario della nascita di Renato Calapso, Messina–Taormina, 1–4 aprile 1981, Roma: Libreria Eredi Virgilio Veschi, pp. 127–152, MR 0698973, Zbl 0958.32504 . A paper where a trace condition for pluriharmonic functions is given.
Fichera, Gaetano (1982b), "Valori al contorno delle funzioni pluriarmoniche: estensione allo spazio 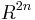$R^{2n}$ di un teorema di L. Amoroso (Boundary values of pluriharmonic functions: extension to the space 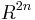$R^{2n}$ of a theorem of L. Amoroso)" (in Italian), Rendiconti del Seminario Matematico e Fisico di Milano 52 (1): 23–34, doi:10.1007/BF02924996, MR 0802991, Zbl 0569.31006 .
Fichera, Gaetano (1982c), "Su un teorema di L. Amoroso nella teoria delle funzioni analitiche di due variabili complesse (On a theorem of L. Amoroso in the theory of analytic functions of two complex variables)" (in Italian), Revue Roumaine de Mathématiques Pures et Appliquées 27: 327–333, MR 0669481, Zbl 0509.31007 .
Fichera, Gaetano (1983), "Sul teorema di Cauchy–Morera per le funzioni analitiche di più variabili complesse (On the theorem of Cauchy–Morera for analytic functions of several complex variables)", Rendiconti della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 74 (6): 7336–350, Zbl 0573.32005 (in Italian). A paper where the Morera theorem for analytic functions of several complex variables is proved, requiring only the local integrability for the given function $f$ .
Fichera, Gaetano (1986), "Unification of global and local existence theorems for holomorphic functions of several complex variables", Memorie della Accademia Nazionale dei Lincei, Classe di Scienze Fisiche, Matematiche e Naturali, 8 18 (3): 61–83, MR 0917525, Zbl 0705.32006 . A paper describing the ideas of (Fichera 1957), giving some extensions of those ideas and a solution for a particular Cauchy problem for holomorphic functions of several variables.
Fichera, Gaetano (1991), "Ricordo di Renato Caccioppoli (Remembering Renato Caccioppoli)", Ricerche di Matematica 40 (supplement): 11–15, Zbl 0788.01051 . Some recollections of his close friend Renato Caccioppoli.
Fichera, Gaetano (1995a), "L'ultima lezione (The last lesson)", Rendiconti della Accademia Nazionale delle Scienze detta dei XL, Memorie di Matematica e Applicazioni 19 (1): 1–24, MR 1387547, http://www.accademiaxl.it/Biblioteca/Pubblicazioni/browser.php?VoceID=2643 (In Italian). His last lesson of the course of higher analysis in occasion of his retirement from university teaching in 1992.
Fichera, Gaetano (1995b), "La nascita della teoria delle diseguaglianze variazionali ricordata dopo trent'anni (The birth of the theory of variational inequalities remembered thirty years later)", Incontro scientifico italo-spagnolo. Roma, 21 ottobre 1993, Atti dei Convegni Lincei, 114, Roma: Accademia Nazionale dei Lincei, pp. 47–53, http://www.lincei.it/pubblicazioni/catalogo/volume.php?lg=e&rid=36500 (in Italian).
Fichera, Gaetano (1996), "Rivisitazione e storia due aspetti contrastanti della storiografia scientifica (Revisitation and history: two conflicting aspects of scientific historiography)", in Tarozzi, Gino, Convegno "Giuseppe Geminiani", Cesena 16–19 October 1995, Cesena–Urbino (in Italian).
Fichera, Gaetano (1997), "A boundary value problem connected with response of semi-space to a short laser pulse", Atti della Accademia Nazionale dei Lincei, Rendiconti Lincei, Matematica e Applicazioni, 9 8 (4): 197–228 . Gaetano Fichera last, postumhous scientific paper, prepared for the publication by Olga Arsenievna Oleinik and his wife.
Günther, Nikolai Maximovich (1967), Potential theory and its applications to basic problems of mathematical physics, New York: Frederick Ungar Publishing, Zbl 0164.41901 . A classical textbook in potential theory: paragraph 24 of chapter const of results proved by Gaetano Fichera in (Fichera 1948).
Severi, Francesco (1931), "Sur une propriété fondamentale des fonctions analytiques de plusieurs variables", Comptes rendus hebdomadaires des séances de l'Académie des sciences 192: 596–599, Zbl 0001.14802, http://gallica.bnf.fr/ark:/12148/bpt6k3145g.image.r=Comptes+rendus.f596.langFR , available at Gallica.
Severi, Francesco (1958), Lezioni sulle funzioni analitiche di più variabili complesse – Tenute nel 1956–57 all'Istituto Nazionale di Alta Matematica in Roma (Lectures on analytic functions of several complex variables – Lectured in 1956–57 at the Istituto Nazionale di Alta Matematica in Rome), Padova: CEDAM – Casa Editrice Dott. Antonio Milani, Zbl 0094.28002 . Notes from a course held by Francesco Severi at the Istituto Nazionale di Alta Matematica (which at present bears his name), containing appendices of Enzo Martinelli, Giovanni Battista Rizza and Mario Benedicty.
Weinberger, Hans F. (1999), "Fichera's method for bounding eigenvalues", Interactions between Analysis and Mechanics. The Legacy of Gaetano Fichera. Convegno internazionale, Atti dei Convegni Lincei, 148, Roma: Accademia Nazionale dei Lincei, pp. 51–65, http://www.lincei.it/pubblicazioni/catalogo/volume.php?lg=e&rid=36500 . (See here for a preprint version available from the Author's website retrieved on 1 May 2009).

External links

Gaetano Fichera at the Mathematics Genealogy Project.
Bonafede, S.; Cialdea, A.; Germano, B. et al., eds. (2007), "3^o Simposio Internazionale Problemi Attuali dell'Analisi e della Fisica Matematica, dedicato alla memoria di Gaetano Fichera – (3rd international symposium on current problems in analysis and mathematical physics dedicated to Gaetano Fichera) Taormina, 29 Giugno–1 Luglio 2006" (in English), Le Matematiche LXII (II), Zbl 1139.74400, http://www.dmi.unict.it/ojs/index.php/lematematiche/issue/view/4 . A volume of the journal published by the Mathematics Department of the University of Catania containing a selection of papers presented to the 3rd international symposium on current problems in analysis and mathematical physics, a periodic conference dedicated to Gaetano Fichera.
"Fichèra, Gaetano" (in Italian), Enciclopedia Treccani, 2008, http://www.treccani.it/enciclopedia/gaetano-fichera/, retrieved 14 April 2011 . The biographical entry about Gaetano Fichera at the Enciclopedia Treccani.
Kiguradze, Ivan; Shervashidze, Tengiz, eds. (2007), "Issue dedicated to the memory of Prof. Gaetano Fichera (1922–1996) on the occasion of his 85th birthday", Georgian Mathematical Journal 14 (1) . Published by the A. Razmadze Mathematical Institute of the Georgian National Academy of Sciences.

Persondata
Name	Fichera, Gaetano
Alternative names
Short description
Date of birth	8 February 1922
Place of birth	Acireale
Date of death	1 June 1996
Place of death	Rome